之前个人理解错误，浮点数转换少了一步。
因为当时看视频和别人博客的时候，发现很多人没有说清楚一些很细致的东西。
首先，浮点数的表示，有

• 定点数据表示
• 浮点数据表示
• IEEE754

定点数据表示

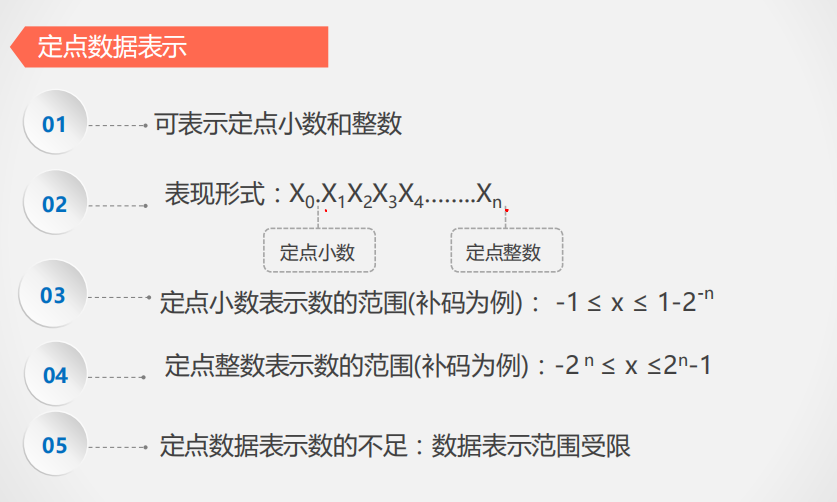
原理是将一个浮点数的整数和小数部分各自转为二进制，最高位表示符号位。
例如使用定点数据表示，表示 -86.25。

86 转为二进制：0_1010110
0.25 转为二进制为 0.01
86.25 二进制为 0_1010110.01
-86.25 = 1_1010110.01
反码 1_0101001.11
补码 1_010_1001.11

所以 -86.25 的定点数据表示为 1_010_1001.11。
要注意的是，有些在线转换二进制的网站，会将 -86.25 转为 -1010101.11，原因在于网站的工具没有对负数就行补一位最高位，也就是说，网站不会对负数转为补码形式。
可以将转换后的二进制数据，反过来生成10进制的数据，就可以测出转换工具的 bug了。

浮点数据表示

浮点数据表示就是

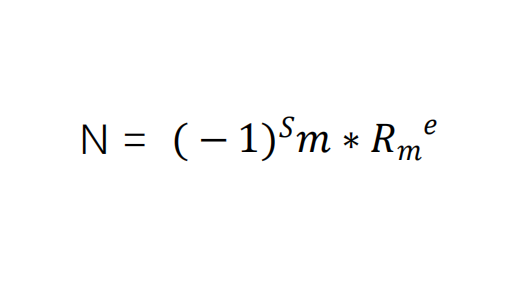
过程看 https://www.cnblogs.com/whuanle/p/12263903.html

IEEE754

IEEE754 跟 浮点数据表示，有差异，IEEE754 表示方法

S	E	M	精度
S	8位偏指数E	23位有效尾数M	单精度
S	11位偏指数E	52位有效尾数M	双精	度

根据 IEEE 754 格式，例如单精度浮点数的表示为：

N = (-1)^S 2^E-127 1.M

浮点数据表示

N = (-1)^S 2^e 1.M

之前看过的很多博客和视频，没有对此进行区分，大多数将 浮点数据表示 当作 IEEE754 了。
另外，浮点数要补足位数时，是从小数部分后面补足的。
例如 8 位表示 0.101B，为 0.101_00000B。

这里

e = E - 127

127 的二进制为 0111 1111。

E = e + 0111_1111
e = E - 0111_1111

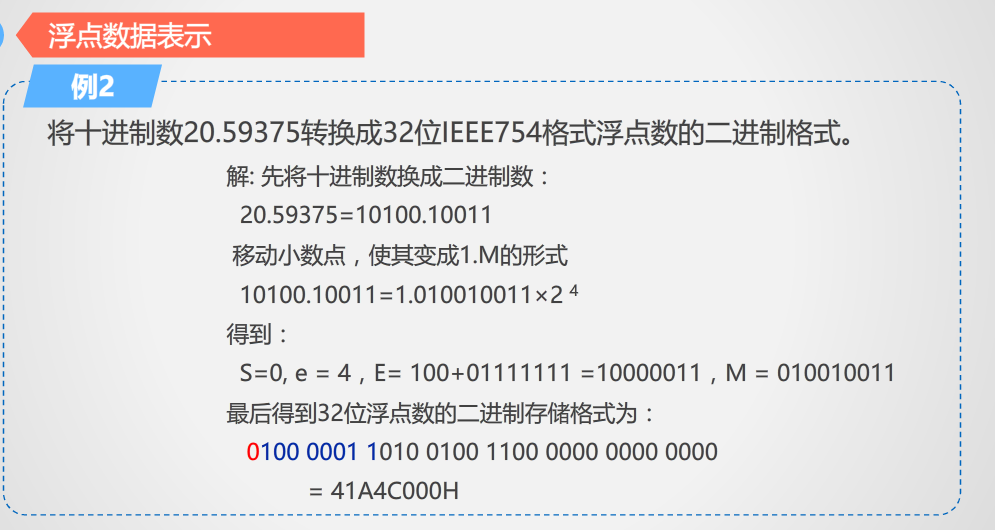
例题如下