Computer System Architecture - Data Representation

Computer System Architecture - Data Representation

Table of Contents

• Computer System Architecture - Data Representation
• Data Representation
• Floating-point Numbers
• Floating-point Standards
• Example Problems
• Computer System Conclusion

Data Representation: Data representation refers to the data types that can be directly recognized and referenced by computer hardware (e.g., fixed-point numbers, floating-point numbers).

Where it manifests: It is manifested in having instructions and functional units that operate on these data types.

Types of Data Structures: Strings, Queues, Lists, Stacks, Arrays, Linked Lists, Trees, Graphs

What is a Data Structure: It reflects the structural relationships between various data elements and/or information units that will be used in applications.

Data Representation

Custom Data Representation

Custom data representation includes identifier-based data representation and data descriptor-based data representation.

Identifier-based Data Representation

Identifier-based data representation refers to using identifiers to denote data types, such as negative numbers, integers, floating-point types, etc.

Principle: Each piece of data in the computer carries a type identifier.

Advantages: It simplifies the instruction system and compiler, facilitating automatic validation and verification of different data types.

Disadvantages: An identifier bit can only describe one piece of data, which is inefficient in terms of description.

We can imagine this as value types in C#.

Data Descriptor-based Data Representation

Similar to identifier-based data representation, the main difference is that in identifier-based data representation, the identifier is packaged with the data; in data descriptor representation, the data descriptor is separated from the data.

The data descriptor contains various flags, lengths, and data addresses.

We can imagine this as reference types in C#.

Floating-point Numbers

For a floating-point number in decimal, we can use the following formula to represent the fractional part:

N = ±m * 10^e

N represents the floating-point number, m represents the mantissa, and e represents the exponent.

For example, 1100.1 = 0.1 * 10^3.

The above applies to decimal representation, whereas in computer systems, binary, octal, and hexadecimal systems are generally used.

Therefore, the formula for computers to represent floating-point numbers is as follows:

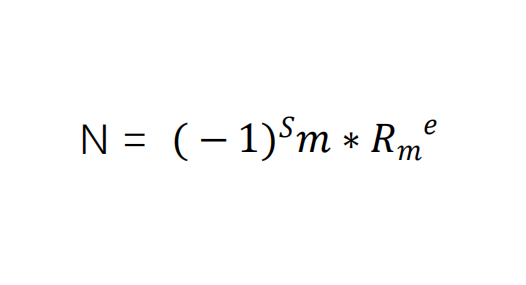
S indicates the sign, with S = 0 representing a positive number and S = 1 representing a negative number.

m is the mantissa.

R_m indicates the base of the exponent.

e represents the value of the exponent.

The storage format of floating-point numbers in data storage units is shown below:

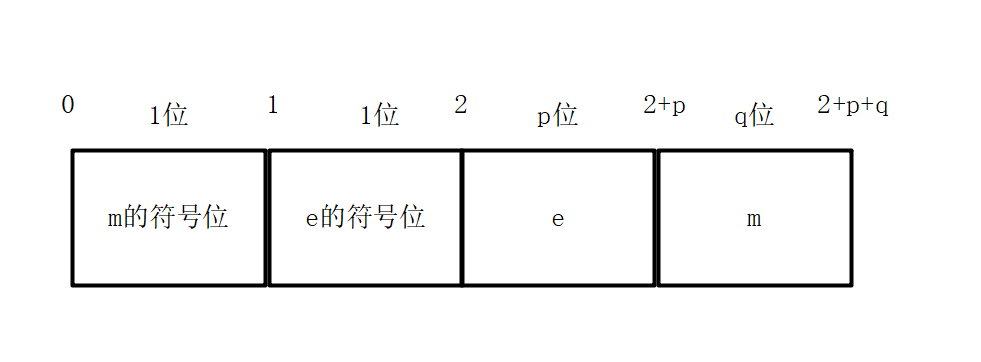
Some books and tutorials combine e_r and e bits together.

The exponent of the floating-point number needs to be biased.

The principle behind this is simply to move the sign bit (positive or negative) that belongs to the mantissa to the front position.

Sign-Magnitude: In a binary number, the highest bit represents the sign, with 0 for positive and 1 for negative; the remaining bits represent the absolute value.

Principle: (-1)^S, where s = 0 means a positive value, and s = 1 means a negative value.

Zero has two representations: positive zero and negative zero.

Two's Complement: Take a number and convert it to sign-magnitude.

If it is a positive number, its two's complement is the same as its sign-magnitude and does not need to be changed.

If it is a negative number, all the bits except the first are inverted, and the last bit is added 1.

Zero has only one representation: positive zero from sign-magnitude.

Excess Notation: Excess notation (also called bias notation) is the sign bit's negation in two's complement. It is typically used to reduce the exponent by 1 for floating-point numbers, introduced to ensure that the floating-point machine code is all zeros.

The sign bits in excess and two's complement are opposites.

For example, convert the number 666666 to octal floating-point format:

666666(int) =  2426052 = 2.426052 * 8^6 

From this, we can see that m = 0.2426052; r_m = 8; e = 6;

The binary representation of octal 2426052 is 00001010 00101100 00101010.

The binary of 6 is 00000110; and its excess notation is 10000110.

Combining these gives us 10000110 + 00001010 00101100 00101010.

Thus, the storage format for 666666 is 0100001100001010 00101100 00101010.

It's important to note that the actual calculations are in binary; the above method is just for clearer understanding of the representation method.

It can be observed that when the number of bits is fixed, a larger bit size for the exponent allows for a broader representable range, albeit with decreased precision; conversely, a smaller bit size for the exponent allows for a narrower range but higher precision.

Floating-point Standards

According to IEEE754, there are two basic floating-point types specified: single precision (float) and double precision (double).

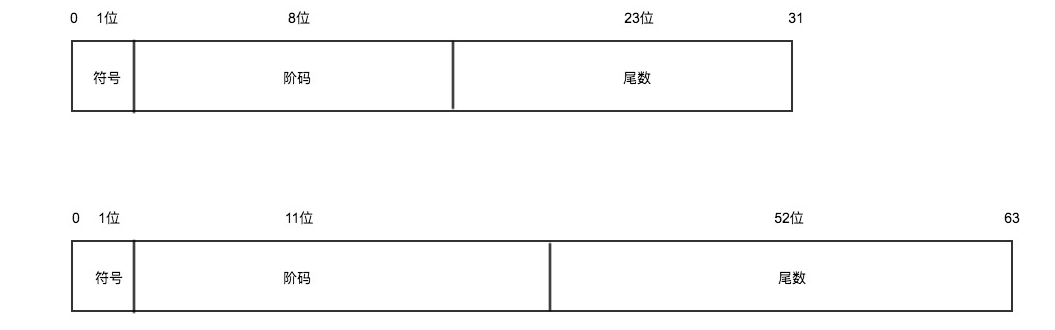
Float

For single precision, the maximum value of the exponent e is 2^8-1, which ranges from -127 to 128 (since negative numbers require a two's complement adjustment).

r_m^e = 2^-127 ~ 2¹²⁸.

2¹²⁸ is the maximum absolute value of r_m^e.

Thus, the upper and lower limit is -3.4028236692094e+38 ~ 3.4028236692094e+38.

Removing extra decimals gives us -3.40E+38 ~ +3.40E+38.

The mantissa range is 2²³ = 8388608, resulting in a total of 7 significant digits.

Hence, the precision of Float is only 7 digits. Since the last digit is often rounded, full accuracy can only be guaranteed for 6 significant digits.

Example Problem

Determine the storage format of -0.666666 in float.

Solution process:

Convert -666666 to binary: 10001010 00101100 00101010. Since it is a negative number, we need its two's complement,

The sign-magnitude is 11110101 11010011 11010101, and the two's complement is 11110101 11010011 11010110.

Returning to the main topic,

-0.666666 = -0.11110101 11010011 11010110,

Shift one position = -1.1110101 11010011 11010110 * 2^-1.

e = -1, represented in binary as 1111 1111, with its excess notation as 0111 1111.

Finally, we have 1 0111 1111 1110101 11010011 11010110.