Differential Mean Value Theorem involves several important theorems:
- Rolle's Theorem
- Lagrange's Mean Value Theorem
- Cauchy's Mean Value Theorem
- L'Hôpital's Rule
Reference: https://www.hanspub.org/journal/PaperInformation?paperID=33661
Rolle's Theorem
Theorem 1 (Rolle) Let the function f(x) satisfy:
(1) Continuous on [a,b];
(2) Differentiable on (a,b);
(3) f(a) = f(b),
then there exists ξ ∈ (a,b) such that f′(ξ) = 0.
The geometric meaning of Rolle's Theorem: A smooth curve with equal heights at both endpoints must have at least one point where the tangent is parallel to the x-axis.
In other words, there is at least one point ξ such that f′(ξ) = 0.
As shown in the figure below:
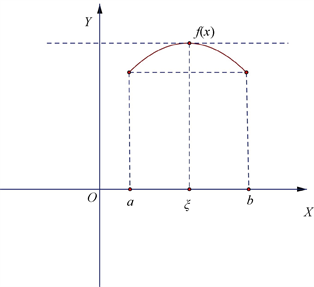
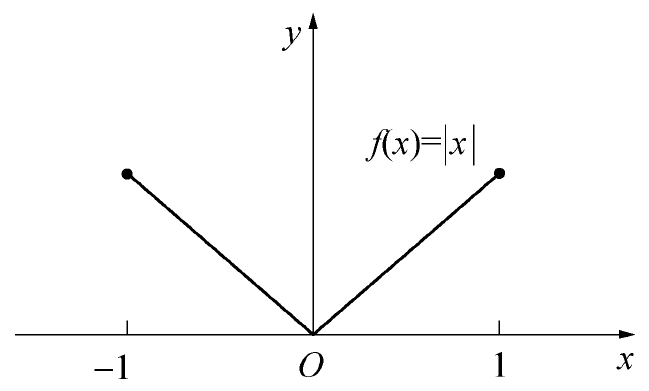
In the figure below, although it is continuous, it is not differentiable, hence it does not satisfy Rolle's Theorem:
Lagrange's Mean Value Theorem
Theorem 2 (Lagrange) Let the function f(x) satisfy:
(1) Continuous on [a,b];
(2) Differentiable on (a,b),
then there exists ξ ∈ (a,b) such that:
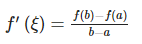
The geometric meaning of Lagrange's Mean Value Theorem is that there must be at least one point on the smooth curve where the tangent line is parallel to the line that connects the endpoints of the curve.
In other words, there is at least one point's tangent along the segment connecting points a and b that is parallel to this straight line.
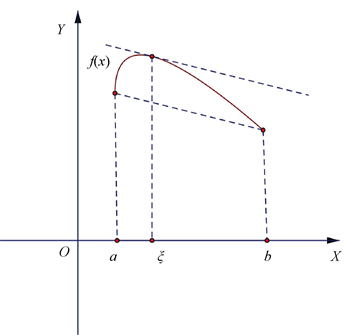
Cauchy's Mean Value Theorem
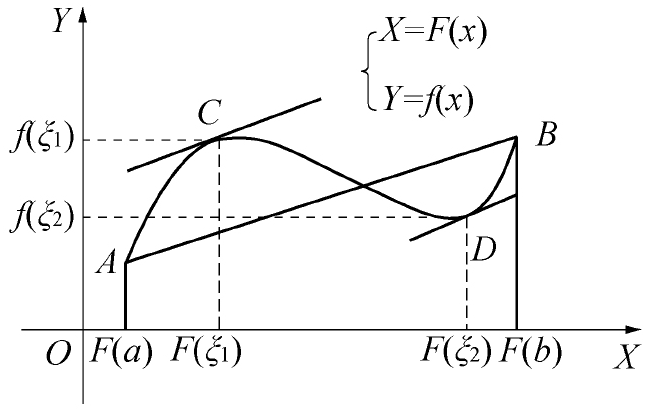
Let the functions f(x) and F(x) satisfy:
(1) Continuous on [a,b];
(2) Differentiable on (a,b);
(3) When x ∈ (a,b), F′(x) ≠ 0 (as shown in Figure 2-23), then there exists at least one point ξ ∈ (a,b) such that:
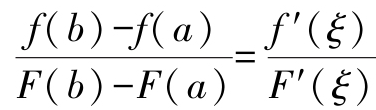

文章评论