内容目录
微分中值定理,涉及了多个重要的定理:
- 罗尔定理
- 拉格朗日中值定理
- 柯西中值定理
- 洛必达法则
参考资料:https://www.hanspub.org/journal/PaperInformation?paperID=33661
罗尔定理
定理1 (Rolle) 设函数 f(x)
满足:
(1) 在 [a,b] 上连续;
(2) 在 (a,b) 内可导;
(3) f(a)=f(b),
则存在 ξ∈(a,b) 使得 f′(ξ)=0 。
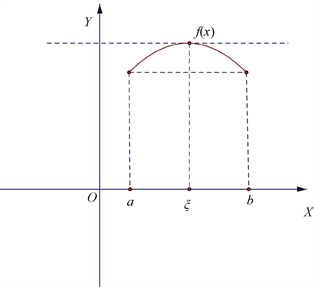
罗尔定理的几何意义:两端点处高度相等的光滑曲线内必有一点处的切线与x-轴平行。
也就是说,至少存在一个点 ξ,f′(ξ)=0。
如图所示:
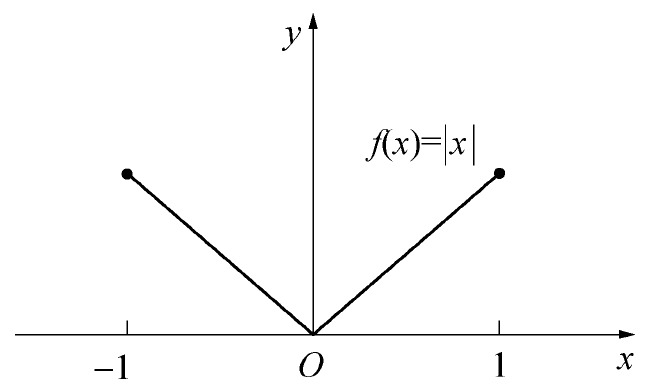
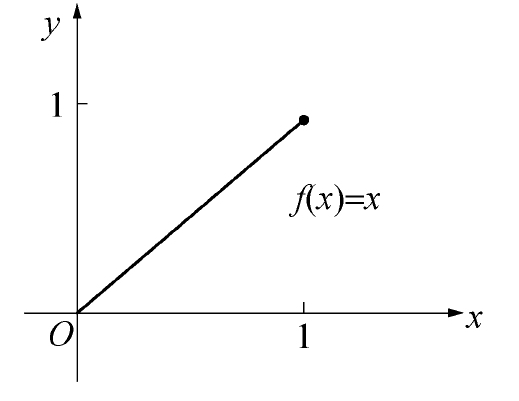
下图中,虽然连续,但是不可导,因此不能符合罗尔定理:
拉格朗日中值定理
定理2( Lagrange) 设函数 f(x)
满足
(1) 在上连续;
(2) 在 (a,b) 内可导,
则存在 ξ∈(a,b) 使得:
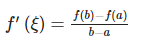
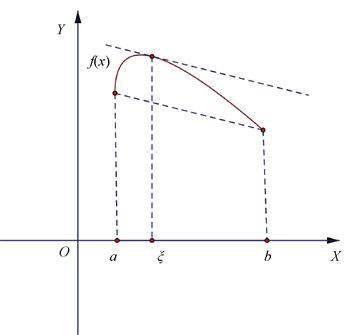
拉格朗日中值定理的几何意义是:光滑曲线内必有一点处的切线平行于连接曲线两端点的直线。
也就是说 x 在 a、b 两点的连线,在曲线内必有一个点的切线跟这条直线平行。
柯西中值定理
设函数 f(x)、F(x) 满足:
- (1)在[a,b]上连续;
- (2)在(a,b)内可导;
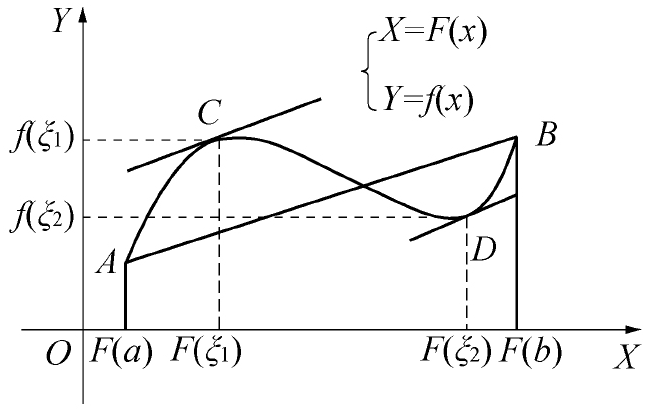
- (3)当x∈(a,b)时,F′(x)≠0(见图2-23),则至少存在一点ξ∈(a,b),使
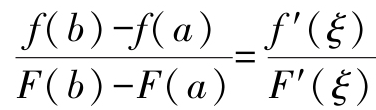

文章评论