学习要求
算法复杂度计算方法
算法时间复杂度和空间复杂度的分析方法。
算法的描述和分析
【1】
数据的运算通过算法(Algorithm)描述的
算法是数据结构课程的重要内容之一。
算法是任意一个良定义的计算过程,它以一个或多个值作为输入,并产生一个或多个值作为输出。因此,算法是一系列将输入转换为输出的计算步骤。
一般地,一个问题的输入实例是满足问题陈述中所给出的限制、为计算该问题的解答所需要的所有输入构成的。若一个算法对于每个输入实例均能终止并给出正确的结果,则称该算法是正确的。正确的算法解决了给定的计算问题。
当然,能够求解一个问题并正确解决的算法有很多种,究竟使用哪种方法来评价这些算法的好坏呢?一般主要考虑以下三点:
- 执行算法所耗费的时间;
- 执行算法所耗费的存储空间;
- 算法应易于理解、易于编码、易于调试等。
在 “底层级语言” 中例如 C 、C+++ 容易做到前两点,但是难以做到第三点;C#、JAVA 这类虚拟机语言可以做到第一第三点,但是运行时较大,当然光论算法存储空间大小可能会很小;Python 、JS 这类弱语言语言,一般 “性能较差”;Rust 解决了 C、C++ 很多缺点,但是学习曲线长、难以理解和编码;貌似 Go 语言做到了这三者均衡,好像现在很多人正在学习 Go 语言(俺也一样)。
编程语言是实现算法的利器,然而哪种语言都很难做到十全十美,但是我们可以根据编程语言的特点,利用其特性取优化代码,实现高性能程序。
一个算法是由多条语句组成的,算法耗费的时间是每条语句的执行时间之和,在这个时间中:
- 每条语句的执行时间是:该语句的执行次数和每次执行时间(平均)的乘积
- 一个语句的执行次数称为频度(Frequencry Count)
在 C#、Java 中有大量的封装方法,在引入其它库的情况下很难确定执行了多少语句,C# 中有 Linq ,一个方法里面可能还嵌套调用了 N 个步骤。因此不太语言之间是很难对比执行了多少语句的。还有其它原因,在 C#、Java 中很难比较一个算法的性能,当然在高级语言中,并不只是排序之类的算法比较,例如比较某个反射算法的性能等,这个时候无法用语句的算法复杂度预测性能,这是可以使用 Benchmark 工具进行测试。
【2】
算法具有由规定的基本运算即运算顺序所构成的完整的解题步骤,算法具有以下特性:
1,有穷性
一个算法必须包装执行有限步骤后结束。
2,确定性
算法的每一个步骤必须有明确的意义。
3,输入
4,输出
5,可行性
【3】
接下来是如何表示算法。
一般地,我们将算法求解问题的输入量称为问题的规模,并且用一个整数表示。例如矩阵乘积问题的规模是矩阵的阶数。
前面提到语句的执行次数称为频度,该算法中所有语句的频度之和使用 T(n) 表示:
for (int j = array.Length - 1; j > 0; j--) // n-1
{
for (int i = 0; i < j; i++) // n(n-1)
{
var sap = array[i]; // n²
array[i] = array[i + 1]; // n²
array[i + 1] = sap; // n²
}
}在忽略一些细节(不准确)的情况下,我们大致计算得:
T(n) = 4n² + 1当然,每个语句的执行速度都是不一样的,这里我们无法计算出时间消耗。但是可以衡量一个算法的复杂度。
时间复杂度 是表示一个算法的时间耗费,是一个关于计算求解问题规模 n 的函数。
当问题的规模趋无穷大时(例如上面代码示例的 array 数组),我们把 T(n) 的数量级称为算法的渐进时间复杂度。
当然我们可以直接得出 n² 这里数量级,因为 ² 是最大的阶数。但是严谨来看,需要一个求解过程,例如:
lim T(n)/n² = lim(4n²-1)/n² = 4
n->∞ n->∞
4n²/n² = 4,4
1/n² = m ,而 0< m < 1因为除于 n² ,该式子能够得出一个不为 0 的常数,我们把这个数量级使用 O(n) 表示。
那么称 T(n) = O(n²) 为此算法的渐近时间复杂度。
但是这样计算,需要掐准每个细节的执行次数,很不方便,而且容易出错,于是可以将基础操作作为计算依据。代码中基本操作如下:
var sap = array[i]; // n²
array[i] = array[i + 1]; // n²
array[i + 1] = sap; // n²因此,可以直接算出是 T(n) = 3n²。
当问题规模较大时,渐近时间复杂度与时间复杂度无限接近,因此我们可以使用渐近时间复杂度来表示时间复杂度。
当求解的问题与 n 无关时,则该算法的时间复杂度为常数阶。
如:
temp = i;
i = j;
j = temp;T(n) = 3,则 T(n) = O(1)。
因此,其时间复杂度为 O(1)。(注意,O(1) 表示其渐近时间复杂度,而不能说是 1 )。
【4】
下面来一些计算示例。
void func(int n)
{
int i, j, x = 0;
for (i = 0; i < n; ++i) {
for (j = i + 1; i < n; j++){
++x;
}
}
}把 x 当作基础操作,x 计算次数是:f(n) = n * (n-1)/2
显然,T(n) = O(n²) 。
【5】
常见的时间复杂度按数量级递增排列依次为:常数 0(1)、对数阶 0(log2n)、线形阶 0(n)、线形对数阶 0(nlog2n)、
平方阶 0(n2)立方阶 0(n3)、k 次方阶 0(nk)、指数阶 0(2n)。
问题规模为 n 是,各种数量级的情况如下:
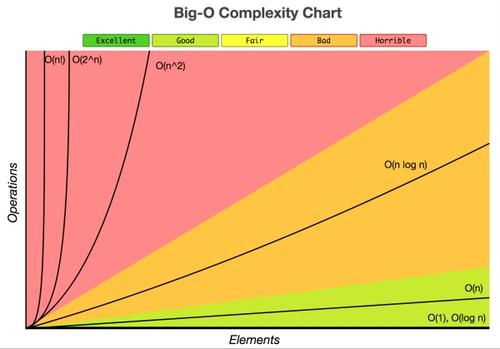
图片来自[xiaoxue.tuxi.com.cn]但是此网站被挂马了,大家别进去。
关于对数的复杂度,可能有些不了解,举个代码例子:
int count = 1;
while(count < n )
count = count * 2;如果 n = ?,执行次数为 ?
n 次数
2 1
4 2
8 3
... ...可知,n = 2^(次数),当 n 趋近于无穷大时,设次数为 m,在坐标轴上都有一点 n,求 m。
此时 根据对数的概念,可知 m = log2 n。
简单来说,如果计算时,有这种变化的情况,可以列一个函数公式或者列一个表替代一些简单的数字进去,发现规律,再使用数学符号表示。

文章评论