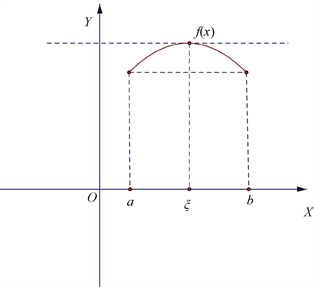
微分中值定理，涉及了多个重要的定理： 罗尔定理 拉格朗日中值定理 柯西中值定理 洛必达法则 参考资料：https://www.hanspub.org/journal/PaperInformation?paperID=33661 罗尔定理 定理1 (Rolle) 设函数 f(x) 满足： (1)[......] 继续阅读

Differential Mean Value Theorem involves several important theorems: Rolle's Theorem Lagrange's Mean Value Theorem Cauchy's Mean Value Theorem L'Hôpi[......] 继续阅读

背景：最近使用 Debezium 做数据库数据监听工具，然后使用 C# 开发管理工具对接 kafka 获取增量同步的数据，这个 C# 管理工具需要支持自定义下游数据库映射，因此再新增加映射关系时需要批量将上游数据全量同步到下游，然后才能从 Kafka 中开始使用增量数据同步，以便保持上下游的数据一致[......] 继续阅读

背景：最近使用 Debezium 作为数据库数据监听工具，并利用 C# 开发管理工具对接 Kafka 来获取增量同步的数据。这个 C# 管理工具需要支持自定义下游数据库映射，因此在新增映射关系时，需要批量将上游数据全量同步到下游，才能从 Kafka 中开始使用增量数据同步，以保持上下游的数据一致性。[......] 继续阅读

首先在 router/index.ts 中创建对应的路由。 const router = createRouter({ history: createWebHistory(import.meta.env.BASE_URL), routes: [ { path: '/',[......]继续阅读

First, create the corresponding routes in router/index.ts. const router = createRouter({ history: createWebHistory(import.meta.env.BASE_URL), rou[......]继续阅读

Kiota 是一个命令行工具，用于将 swagger、openapi 生成对应语言的的代码文件，目前支持： .NET CLI(C# 的 System.CommandLine) Go Java PHP Python TypeScript/JavaScript 官方文档： https://learn[......] 继续阅读

Kiota is a command-line tool used to generate code files in various programming languages from Swagger and OpenAPI specifications. Currently, it suppo[......] 继续阅读

[TOC] 导读 最近一个数据分析朋友需要学习 Hive，刚好我也想学，便利用手头的服务器搭建一个学习环境，但是搭建过程中，发现网上的教程很多过时了，而且部署过程中，很多地方走不通，博主也没有给出对应的说明。花了大力气才从各种资料中完成 Hadoop、Mysql、Hive 三者的部署。 因此，本文记[......] 继续阅读

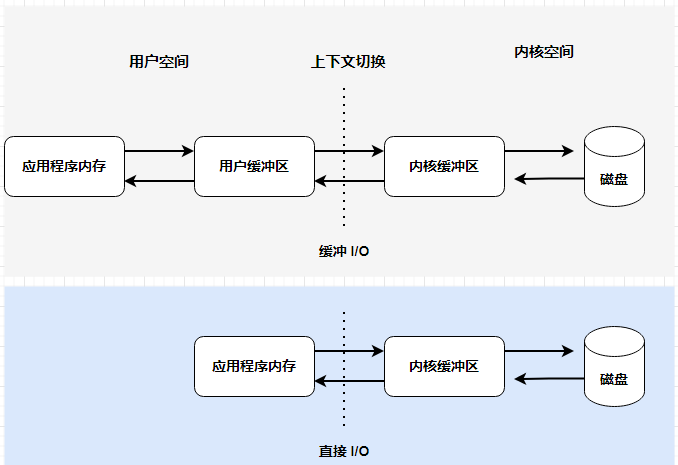
通常程序执行 IO 操作时，需要涉及用户空间和内核空间的两个缓冲区。 Only the kernel can operate with hardware such as disks; therefore, when data flows to the program, it must first r[......] 继续阅读

通常程序执行 IO 操作时，需要涉及用户空间和内核空间的两个缓冲区。 只有内核才能跟磁盘等硬件进行操作，因此数据在流向程序时，必定会先存在于内核缓冲区，内核缓冲区又称为 PageCache，不同操作系统的 PageCache 机制不一样。 内核缓冲区：系统内核在内核空间中定义的内核缓冲区，即 Pa[......] 继续阅读

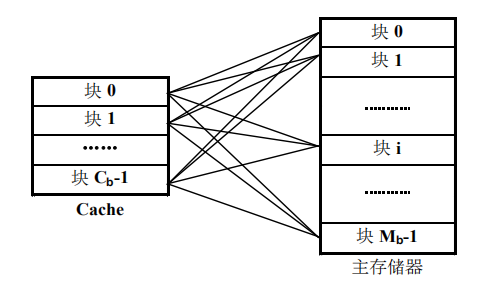
首先映射是按照块来映射的，每个块内都有一个块内地址，记录每个字长的位置。 本文部分图片来源参考：https://blog.csdn.net/weixin_42649617/article/details/105092395 直接映射 特点是内存与 Cache 之间的映射位置是固定的，其中内存到[......] 继续阅读

首先映射是按照块来映射的，每个块内都有一个块内地址，记录每个字长的位置。 本文部分图片来源参考：https://blog.csdn.net/weixin_42649617/article/details/105092395 直接映射 特点是内存与 Cache 之间的映射位置是固定的，其中内存到[......] 继续阅读

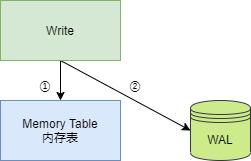
[TOC] 笔者前段时间在学习数据结构时，恰好听说了 LSM Tree，于是试着通过 LSM Tree 的设计思想，自己实现一个简单的 KV 数据库。 代码已开源，代码仓库地址：https://github.com/whuanle/lsm 笔者使用 Go 语言来实现 LSM Tree 数据库，因为[......] 继续阅读

题目： 给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。 示例 1： 输入：nums = [1,2,3,1] 输出：true 示例 2： 输入：nums = [1,2,3,4] 输出：false 示例 3： 输入：n[......] 继续阅读

Title: Given an integer array nums. Return true if any value appears at least twice in the array, and return false if every element is distinct. Examp[......] 继续阅读

During the New Year's holiday, I studied some domain-driven design knowledge. Here is a summary. In domain-driven design, layered architecture is an i[......] 继续阅读

过年假期在学习了一些领域驱动知识，这里做个汇总。 在领域驱动设计中，程序进行分层，是其重要的一部分，因此这里以分层开始，逐步了解 DDD 中的一些概念。 数据映射层 首先第一步是数据库，数据库这一部分是持久层，负责实体对象和数据库表的映射以及数据库连接配置、数据库上下文配置、ORM 配置等，数据库和[......] 继续阅读

分库分表 一般来说，数据库分库分表，有以下做法： 按哈希分片：根据一条数据的标识计算哈希值，将其分配到特定的数据库引擎中； 按范围分片：根据一条数据的标识（一般是值），将其分配到特定的数据库引擎中； 按列表分片：根据某些字段的标识，如果符合条件则分配到特定的数据库引擎中。 分库分表的[......] 继续阅读